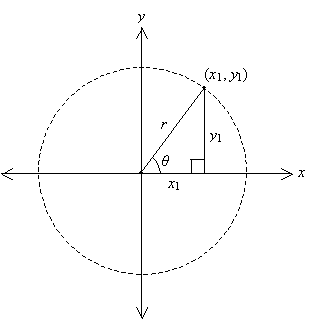
To solve geometry problems about circles, you will need to know the following circle theorems involving tangents, secants, and chords. These theorems can be used to find information about angles, intercepted arcs, and length of segments of a circle. In addition, you find the standard and general form of a circle, the formulas for area and circumference, and the area of a sector of a circle.
Circle formulas
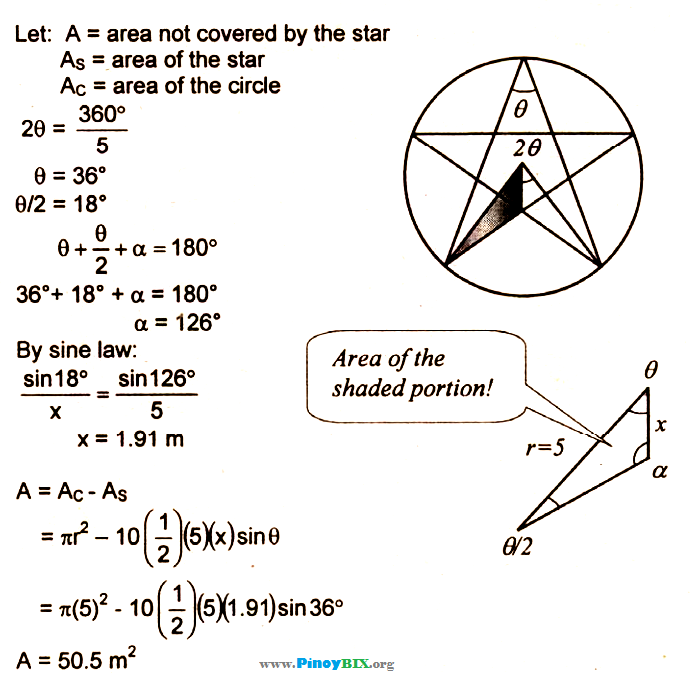
The circumference of a circle equals
The area of a circle equals
The area of a sector equals
Standard form of a circle:
General form of a circle:
Define trigonometric ratios and solve problems involving right triangles. G-C: Understand and apply theorems about circles. This lesson also relates to the following Standards for Mathematical Practice in the Common Core State Standards for Mathematics, with a particular emphasis on Practices 2, 3, and 7: 1. Make sense of problems and persevere. The formula for circumference is C = 2πr C = 2 π r The formula for area of a circle is A =πr2 A = π r 2 Remember, that we approximate π π with 3.14 3.14 or 22 7 22 7 depending on whether the radius of the circle is given as a decimal or a fraction. B C BC B C is tangent to both a circle with center at A A A and a circle with center at D D D. The area of the circle with center at A A A is 225 π 225 pi 2 2 5 π and the area of the circle with center at D D D is 36 π 36 pi 3 6 π. If B C = 16 BC=16 B C = 1 6, find the distance between the centers of the two circles.
Vertical Angles Problem Solving
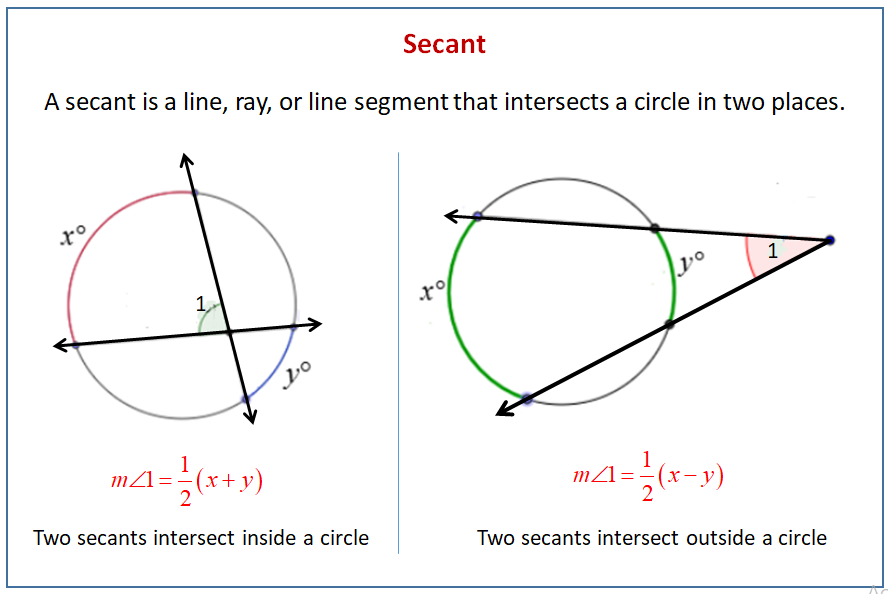
Circle theorems involving angles
The central angle equals the intercepted arc.
An inscribed angle equals
The interior vertical angles formed by two intersecting chords equal
An exterior angle equals
A line tangent to a circle is perpendicular to the radius drawn to the point of tangency.
Solving Angles Problems
Circle theorems involving lengths of segments
Math Problem Solving
When a tangent and secant are drawn from the same exterior point,
When two secants are drawn from the same exterior point,
